拓扑排序

之前做本科毕设的时候，不知道复杂的调度前后约束怎么编码输入到程序里，为此苦恼了许久，现在想想答案就在那里只是我没有去想罢了，它就是——拓扑排序。

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。

1. 理论知识

1.1 有向无环图

有向无环图(Directed Acyclic Graph简称DAG)指的是一个无回路的有向图。其中：

• 有向：两个节点之间的链接有方向
• 无环：图中不存在闭环

如下就是一个有向无环图。

拓扑图，拓扑结构图（TOPOLOGY）

1.2 拓扑排序

即对DAG中的节点排序，

条件：

1. 每个顶点出现且只出现一次。

2. 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

只有对有向无环图（DAG）才有拓扑排序。

步骤：

1. 将边与边的关系确定，建立好入度表和邻接表。
2. 从入度为0的点开始删除，如上图显然是1的入度为0，先删除。
3. 更新入度表，若存在入度为0的点回到第二步。
4. 若节点删除完，则得到拓扑排序结果，如下图得到排序结果为{ 1, 2, 4, 3, 5 }。

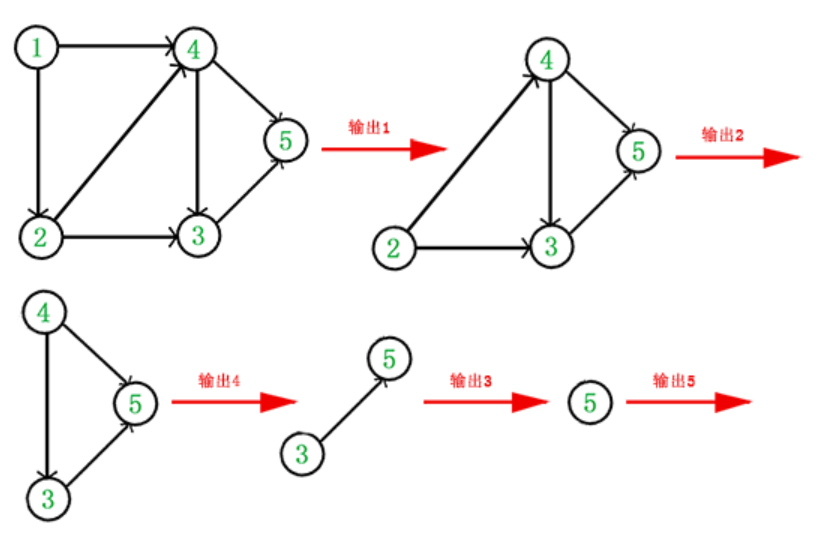
5. 若某一步存在所有点入度都不为0，则此图为有环图，如下图环中的节点入度都为1。

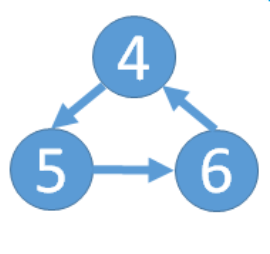
通常，一个有向无环图可以有一个或多个拓扑排序序列。因为同一入度级别的点可以有不同的排序方式。

2. python实现

2.1 介绍

networkx是Python的一个包，用于构建和操作复杂的图结构，提供分析图的算法。图是由顶点、边和可选的属性构成的数据结构，顶点表示数据，边是由两个顶点唯一确定的，表示两个顶点之间的关系。

matplotlib是从matlab移植过来的用于数学计算画图的包，这里不做过多介绍。

在命令行下通过pip安装networkx：

pip install pillow

2.2 基本用法

这里仅限于拓扑图相关的用法。

import networkx as nx
import matplotlib.pyplot as plt

# 构建图
# G = nx.Graph() # 无向图
G = nx.DiGraph()  # 有向图
G.add_node('A')  # 添加点
G.add_nodes_from(['B', 'C', 'D'])  # 批量添加点
G.add_edge('A', 'B')  # 添加边
G.add_edges_from([('A', 'D'), ('C', 'B')])  # 批量添加边

# 拓扑排序
print(G.in_degree)  # 入度
# [('A', 0), ('B', 1), ('C', 1), ('D', 1)]
s = list(topological_sort(G))  # 拓扑排序
print(s)  # ['A', 'D', 'B', 'C']
all_s = list(all_topological_sorts(G))  # 所有拓扑排序
print(all_s)  # [['A', 'D', 'B', 'C'], ['A', 'B', 'C', 'D'], ['A', 'B', 'D', 'C']]


#画图
nx.draw(
    G,
    with_labels=True,
    node_color='y',
)
plt.show()

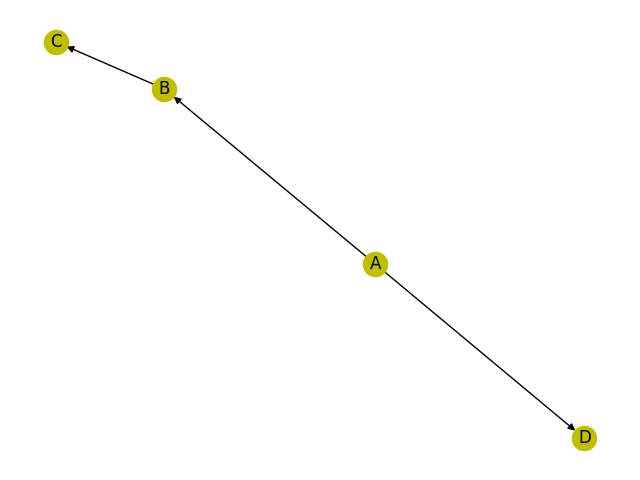
画出的图并不美观，每次运行都不一样，但结构是一样的。

3 解决实际问题

3.1 用矩阵表示前后约束关系

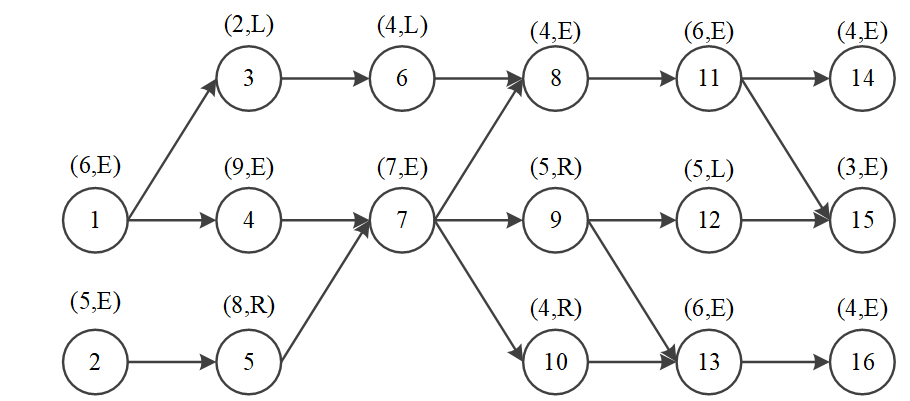
以下图所示的生产问题为例，节点表示工序，节点间的顺序表示前后约束关系。节点上的数字不用管。

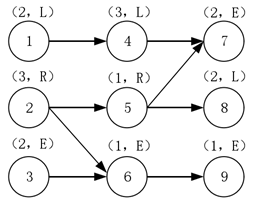
节点之间约束关系可以用01矩阵可以很好的表达并编码。如下所示，a[0][3]==1表示节点1和4之间存在顺序约束，0表示没有约束。

a = np.array([[0, 0, 0, 1, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 1, 0, 0, 0],
            [0, 0, 0, 0, 0, 1, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 1, 0, 0],
            [0, 0, 0, 0, 0, 0, 1, 1, 0],
            [0, 0, 0, 0, 0, 0, 0, 0, 1],
            [0, 0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0, 0]])

3.2 通过计算入度，结合递归的思想来进行拓扑排序

如下：

st=>start: 开始
init=>operation: 初始化有向无环图DAG
select=>operation: 1.计寻找所有入度为0的点作为候选集
2.在候选集中选择点，记录作为路径
3.在DAG图中删除该节点
cond=>condition: 是否遍历完成
e=>end: 结束

st->init->select->cond
cond(no)->select
cond(yes)->e